攻击条件

当两个用户使用相同的模数N、不同的私钥时，加密同一明文消息时，即存在同模攻击

攻击原理

设两个用户的公钥分别为e1和e2，且两者互质。明文信息为m，密文分别为:

​

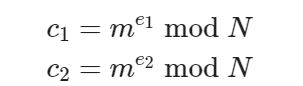
当攻击者截获c1和c2后，就可以恢复出明文。用扩展欧几里得算法求出re1+se2=1 mod n 的两个整数r和s，由此可得:

​

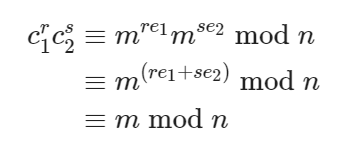
例题

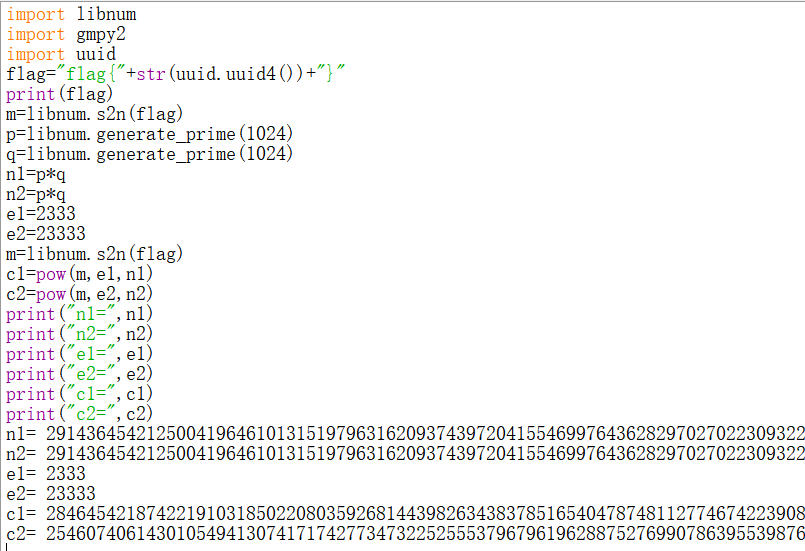
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import gmpy2
from Crypto.Util.number import *
#数字n、c1、c2都太长了，我直接去了
n=
e1= 2333
e2= 23333
c1=
c2=
gcd, s, t = gmpy2.gcdext(e1, e2)
#广义欧几里得求出s,t  gcdext返回值为e1,e2最大公因数和s、t。 s*e1+t*e2=(e1,e2)

#s和t中必然有一位负数，将其变为正数，要使等式仍然成立，取逆元
if s < 0:
    s = -s
    c1 = gmpy2.invert(c1, n)
if t < 0:
    t = -t
    c2 = gmpy2.invert(c2, n)
plain = gmpy2.powmod(c1, s, n) * gmpy2.powmod(c2, t, n) % n
print(long_to_bytes(plain))
#将long转换成字符串，是Crypto.Util.number中的方法，这里用不了libnum.n2s(plain)因为plain太长了

gmpy2常用函数

  • n=invert(m,phi)求mod phi的逆元
  • pow(m,e,n)求c^d mod n
  • gmpy2.is_prime(n) 素性检测
  • gmpy2.gcd(a,b) 欧几里得算法，最大公约数
  • gmpy2.gcdext(a,b) 扩展欧几里得算法
  • gmpy2.iroot(x,n) x开n次根
  • gmpy2.mpz(n) 初始化一个大整数

libnum常用函数

  • libnum.invmod(a,b) 求mod b的逆元

  • 数字型（不论是十六进制还是十进制）与字符串之间的转换：

1
2
3
4
5
6
7
8
import libnum
s="flag{pcat}"
print libnum.s2n(s)


import libnum
n=0x666c61677b706361747d
print libnum.n2s(n)
  • 二进制与字符串之间的转换：
1
2
3
4
5
6
7
8
9
10
import libnum
b=‘01110000011000110110000101110100‘
print libnum.b2s(b)
#二进制的位数最好是8的倍数


import libnum
b=‘01110000011000110110000101110100‘
print libnum.b2s(b)
#二进制的位数最好是8的倍数
  • 质数&因数分解
1
2
3
print libnum.generate_prime(1024)

print libnum.factorize(1024)

本篇博客大部分摘自CTFwiki，记录的目的是为了加深自己的理解，也是为了方便自己的使用