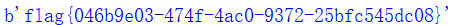不记录直接可以套脚本写出来的
风二西RSA_1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| import gmpy2
import libnum
import uuid
flag="flag{"+str(uuid.uuid4())+"}"
print(flag)
m=libnum.s2n(flag)
p=libnum.generate_prime(512)
q=libnum.generate_prime(512)
n=p*q
e=1
c=pow(m,e,n)
print("n=",n)
print("c=",c)
print("e=",e)
n= 已给出太长我省略了
c= 已给出太长我省略了
|
直接print(long_to_bytes(c))即可
因为long_to_bytes之后前面会多出‘b,就像下面这样
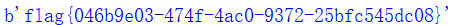
1
2
3
4
5
6
7
8
9
10
| from Crypto.Util.number import *
e=1
n =
c =
for i in range(10000000000000000):
x=str(long_to_bytes(c+n*i))
if x[2]=='f':
print(x)
break
|
风二西RSA_2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| import gmpy2
import libnum
import uuid
flag="flag{"+str(uuid.uuid4())+"}"
print(flag)
m=libnum.s2n(flag)
p1=libnum.generate_prime(64)
q1=libnum.generate_prime(64)
p2=libnum.generate_prime(64)
q2=libnum.generate_prime(64)
p3=libnum.generate_prime(64)
q3=libnum.generate_prime(64)
e=1
c1=pow(m,e,p1*q1)
c2=pow(m,e,p2*q2)
c3=pow(m,e,p3*q3)
print("n1=",p1*q1)
print("c1=",c1)
print("n2=",p2*q2)
print("c2=",c2)
print("n3=",p3*q3)
print("c3=",c3)
n1= 172774622114813683746188230007837413819
c1= 170260248491697016437095929037490480036
n2= 160333927436069409658483084503168246581
c2= 45134242975344810542214361639231372051
n3= 170109598387116572557100744899522621873
c3= 47903985600747367026642413789127948969
|
m=c1 % n1
m=c2 % n2
m=c3 % n3
又n1、n2、n3两两互素,中国剩余定理(不知道有没有可以直接计算中国剩余定理的函数,我没有找到)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| from gmpy2 import *
from Crypto.Util.number import *
n1 = 172774622114813683746188230007837413819
c1 = 170260248491697016437095929037490480036
n2 = 160333927436069409658483084503168246581
c2 = 45134242975344810542214361639231372051
n3 = 170109598387116572557100744899522621873
c3 = 47903985600747367026642413789127948969
print(gcd(n1,n2),gcd(n1,n3),gcd(n2,n3))
M1=n2*n3
M11=invert(M1,n1)
M2=n1*n3
M21=invert(M2,n2)
M3=n1*n2
M31=invert(M3,n3)
m=(c1*M1*M11+c2*M2*M21+c3*M3*M31)%(n1*n2*n3)
print(long_to_bytes(m))
|
风二西RSA_4 (密钥读取)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| from Crypto.PublicKey import RSA
import libnum
import gmpy2
with open("Pubckey.pem","rb") as f: #这个公钥打开之后发现其实是密钥
key=RSA.import_key(f.read())
print('n=%d' % key.n)
print('e=%d' % key.e)
print('d=%d' % key.d)
print('p=%d' % key.p)
print('q=%d' % key.q)
with open("flag.pem",'rb') as f1:
print('c='+str(libnum.s2n(f1.read())))
n=
e=65537
d=
p=
q=
c=
m=pow(c,d,n) #注意这个m不是int型的!!
print(libnum.n2s(int(m)))
|
RSA5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| from Crypto.PublicKey import RSA
import libnum
import gmpy2
with open("pubckey1.pem","rb") as f:
key=RSA.import_key(f.read())
print('n=%d' % key.n)
print('e=%d' % key.e)
with open("flag1.pem",'rb') as f1:
print('c='+str(libnum.s2n(f1.read())))
n=
e=65537
c=
p =
q =
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
|
RSA8
给出n、e、c,但n是素数
phi=(n-1) #这点我没有想到😜
1
2
3
4
5
6
7
8
9
| import gmpy2
import libnum
n= 161670795418661108941395547760068053355832555077779027853700140442876298077926786030806243269042521234383793929910836023913994987010924339006536693866763078849189869497871752489277315727669547511079303136326388638480680630822677173084810848784554433394382029956739707395702556105138001868786944077871569844771
c= 91652340468387584012845155237237896957786753396661434559421169499111938419733760364914054180181470453332534789456757372866493406817246725731113863637159054175158914882334950110118713886213759125279941357012004180349611604118066085014934218543579248275421019690815403585470855502464076600672369539603525850924
e= 65537
phi=n-1
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)).decode())
|